Fuzzy membership functions

How do we define them?

The fuzzy membership functions compute the element's degree of the membership to a given fuzzy set. This measurement is numerically presented as the value between 0 and 1.

Supported functions

At the moment, the ITL supports six different types of the fuzzy membership functions. The linear membership function is often used and IDL has an ability to automatically recognize the type of the linear fuzzy function based on provided parameters. Five other supported functions include Trapezoidal, Triangular, Gauss, Gauss2 and Sigmoidal fuzzy membership functions.

Rising slope — type 1

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} 0,& \text{ if } v_i \leq a_i \\ \frac{v_i-a_i}{b_i-a_i},& \text{ if } a_i < v_i < b_i \\ 1,& \text{ if } v_i \geq b_i \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the lower limit of the worst metric value,
• \(b_i\) - is the starting point of best metric value,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

The following graph represents an example of the rising slope fuzzy function:

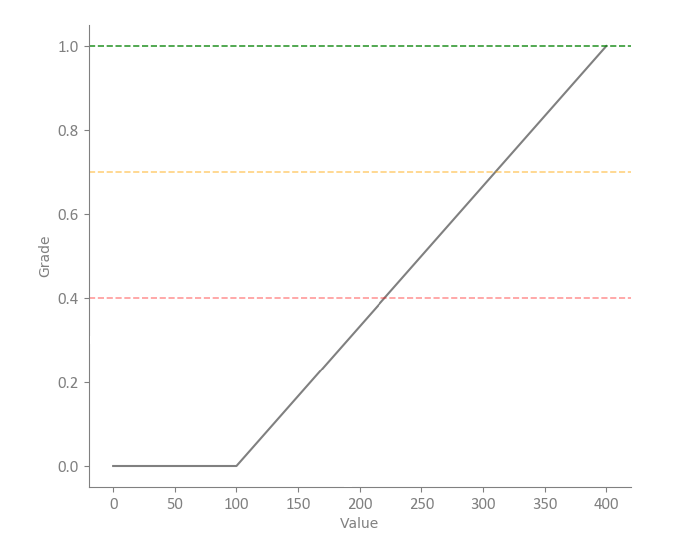
Note how the function starts rising after value of 100 (so the parameter a here equals 100) and has an linear increasing value up to 400. After this point the grade (y-axis) has the constant value of 1.0 (so the parameter b here equals to 400).

Falling slope — type 2

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} 1,& \text{ if } v_i \leq a_i \\ 1-\frac{v_i-a_i}{b_i-a_i},& \text{ if } a_i < v_i < b_i \\ 0,& \text{ if } v_i \geq b_i \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the upper limit of the best metric value,
• \(b_i\) - is the starting point of the worst metric value,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

The following graph represents an example of the falling slope fuzzy function:

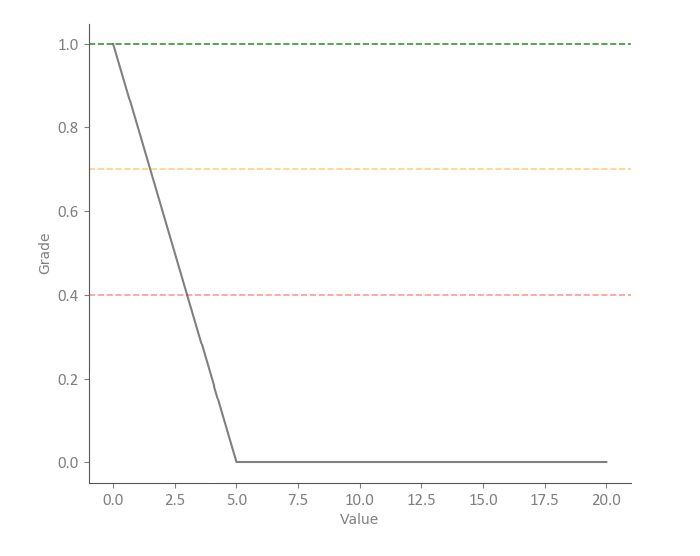
Note how the function immediately starts falling until value of 5 (so the parameter a here equals 0) After this point the grade (y-axis) has the constant value of 0.0 (so the parameter b here equals to 5).

Trapezoidal

Positive

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} 0,& \text{ if } v_i \leq a_i \\ \frac{v_i-a_i}{b_i-a_i},& \text{ if } v_i \in [a_i,b_i) \\ 1,& \text{ if } v_i \in [b_i,c_i] \\ \frac{v_i-d_i}{c_i-d_i},& \text{ if } v_i \in (c_i,d_i] \\ 0,& \text{ if } v_i > d_i \\ \end{cases}\)

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the left upper limit of the worst metric value,
• \(b_i\) - is the starting point of the best metric value,
• \(c_i\) - is the ending point of the best metric value,
• \(d_i\) - is the right lower limit of the worst metric value,
• \(\mu_{F_i}(v_i)\) - is the \(i\)-th metric’s grade between 0 and 1.

Negative

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} 1,& \text{ if } v_i \leq a_i \\ \frac{v_i-b_i}{a_i-b_i},& \text{ if } v_i \in (a_i,b_i] \\ 0,& \text{ if } v_i \in (b_i,c_i) \\ \frac{v_i-c_i}{d_i-c_i},& \text{ if } v_i \in [c_i,d_i) \\ 1,& \text{ if } v_i \ge d_i \\ \end{cases}\)

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the left upper limit of the best metric value,
• \(b_i\) - is the starting point of the worst metric value,
• \(c_i\) - is the ending point of the worst metric value,
• \(d_i\) - is the right lower limit of the best metric value,
• \(\mu_{F_i}(v_i)\) - is the \(i\)-th metric’s grade between 0 and 1.

Triangular

Positive

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} 0,& \text{ if } v_i < a_i \\ \frac{v_i-a_i}{b_i-a_i},& \text{ if } v_i \in [a_i,b_i) \\ 1,& \text { if } v_i = b_i \\ \frac{c_i-v_i}{c_i-b_i},& \text{ if } v_i \in (b_i,c_i] \\ 0,& \text{ if } v_i > c_i \\ \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the left upper limit of the worst metric value,
• \(b_i\) - is the best metric value point,
• \(c_i\) - is the lower limit of the worst metric value,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Negative

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} 1,& \text{ if } v_i \leq a_i \\ \frac{b_i-v_i}{b_i-a_i},& \text{ if } v_i \in (a_i,b_i) \\ 0,& \text { if } v_i = b_i \\ \frac{v_i-b_i}{c_i-b_i},& \text{ if } v_i \in (b_i,c_i) \\ 1,& \text{ if } v_i \geq c_i \\ \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the left upper limit of the best metric value,
• \(b_i\) - is the worst metric value point,
• \(c_i\) - is the right lower limit of the best metric value
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Gaussian

Experimental

Positive

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} {e^{-(\frac{v_i-\mu_i}{\sigma_i})}}^2, &\text { if } v_i \in [\mu_i-6\cdot \sigma_i)\\ 1, &\text { if } v_i = \mu_i\\ {e^{-(\frac{v_i-\mu_i}{\sigma_i})}}^2, &\text { if } v_i \in [\mu_i+6\cdot \sigma_i)\\ \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(\mu_i\) - is the best value metric point ,
• \(\sigma_i\) - is the standard deviation,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Negative

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} {1-e^{-(\frac{v_i-\mu_i}{\sigma_i})}}^2, &\text { if } v_i \in [\mu_i-6\cdot \sigma_i)\\ 0, &\text { if } v_i = \mu_i\\ {1-e^{-(\frac{v_i-\mu_i}{\sigma_i})}}^2, &\text { if } v_i \in [\mu_i+6\cdot \sigma_i)\\ \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(\mu_i\) - is the worst value metric point,
• \(\sigma_i\) - is the standard deviation,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Gaussian 2 (combined)

Experimental

Positive

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} {e^{-(\frac{v_i-\mu_{1_i}}{\sigma_{1_i}})}}^2, &\text { if } v_i \in [\mu_{1_i}-6\cdot \sigma_{1_i})\\ 1, &\text { if } v_i \in [\mu_{1_i}, \mu_{2_i}]\\ {e^{-(\frac{v_i-\mu_{2_i}}{\sigma_{2_i}})}}^2, &\text { if } v_i \in [\mu_{2_i}+6\cdot \sigma_{2_i})\\ \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(\mu_{1_i}\) - is the best metric starting point,
• \(\mu_{2_i}\) - is the best metric ending point,
• \(\sigma_{1_i}\) - is the first distribution standard deviation,
• \(\sigma_{2_i}\) - is the second distribution standard deviation,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Negative

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i)= \begin{cases} {1-e^{-(\frac{v_i-\mu_i}{\sigma_i})}}^2, &\text { if } v_i \in [\mu_i-6\cdot \sigma_i)\\ 0, &\text { if } v_i = \mu_i\\ {1-e^{-(\frac{v_i-\mu_i}{\sigma_i})}}^2, &\text { if } v_i \in [\mu_i+6\cdot \sigma_i)\\ \end{cases}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(\mu_{1_i}\) - is the left upper limit of the best metric,
• \(\mu_{2_i}\) - is the right limit of thr best metric,
• \(\sigma_{1_i}\) - is the first distribution standard deviation,
• \(\sigma_{2_i}\) - is the second distribution standard deviation,
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Sigmoidal

Experimental

Positive

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i) = \frac{1}{1+e^{-b_i \cdot (v_i-a_i)}}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the center value of sigmoid where it equals 0.5,
• \(b_i\) - is the width of sigmoidal region about \(a_i\),
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.

Negative

This fuzzy membership function can be defined as:

\(\mu_{F_i}(v_i) = 1-\frac{1}{1+e^{-b_i \cdot (v_i-a_i)}}\)

where:

• \(v_i\) - is the measured value to be assessed,
• \(a_i\) - is the center value of sigmoid where it equals 0.5,
• \(b_i\) - is the width of sigmoidal region about \(a_i\),
• \(\mu_{F_i}(v_i)\) - is the \(i\)−th metric’s grade between 0 and 1.